European Training Network for the Design and Recycling of Rare-Earth Permanent Magnet Motors and Generators in Hybrid and Full Electric Vehicles (DEMETER)AUTHOR: Adolfo Garcia
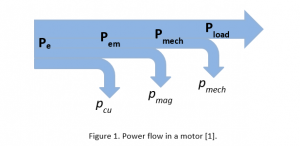
In electrical machines, the aim is generally to attain the highest possible efficiency. Efficiency is given by the ratio of the output power and the input power (Pload and Pe in figure 1). That is, the efficiency will be higher if a reduction of the losses in the system pcu, pmag and pmech is achieved. Typically, the losses in an electrical machine are the winding losses pcu, the core losses pmag and the mechanical losses pmech. Winding losses have a large value at high currents due to Joule effect (I2R), R being the resistance of the windings and I is the current flowing through them. Core losses are composed by iron losses in the electrical steel of the stator. Mechanical losses are generated in the rotor. These are generally composed by the magnet losses, windage losses, bearing losses, etc. In general, mechanical losses are lumped into one category given that their segregation is a cumbersome task.
Core losses can be divided into two main types: hysteresis losses and eddy current losses. The former are due to the movement of the ferromagnetic domains when these align with the time changing flux. The latter are generated by the changing flux circulating in the material. Eddy currents are the main reason behind the use of steel laminations in the magnetic systems of most, if not all, electrical machines (e.g., transformers, motors, actuators, etc.). Figure 2 illustrates the decrease of the eddy currents with the reduction of the thickness in a solid conductor. By reducing the thickness of the material, the eddy currents are forced to flow in a reduced trajectory, thus reducing their amplitude.
Figure 2. Lamination restrains eddy currents and reduces power wastage- a simplified model [2].
Figure 3 shows the behavior of eddy current losses with frequency. It shows that the losses vary with the square of the frequency. Consequently, the core losses might increase in a machine running at high speed. In a rotating electrical machine, speed and frequency are proportional. Mathematically, this is given by the expression n = 120 f / 2p. Where n is the mechanical speed in revolutions per minute (rpm), f is the frequency and 2p is the total number of poles of the machine.
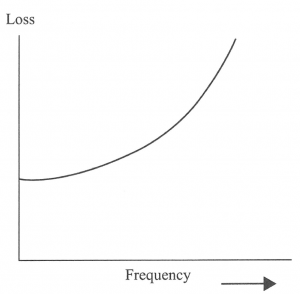
Figure 3. Rise in core losses with frequency [3].
In order to reduce or mitigate the losses due to eddy currents, the laminations are required to be as thin as possible and have a large resistivity. In electrical machines, there are a set number of materials for the design of the magnetic systems–from the conventional SiFe electrical steels with Oriented and Non-Oriented Grains (GO and NO) to Nickel Irons (NiFe), Cobalt Irons (CoFe), Composite materials, Microcrystalline alloys and Amorphous metals.
Figure 4. Niche applications of soft magnetic materials [4].
Amorphous metals
In addition to the reduction of the losses as a goal in the design of electrical machines, the increment of the permeability is of interest, since it dictates how easily the material is magnetized. To increase the permeability one must bolster the perfect crystal orientation and the purity of the metals. Another alternative is to cool a metallic alloy at a rate of millions degrees Celsius per second so that the material becomes solid without the presence of crystallization. Hence, energy minimization associated with regular crystal formation in the atoms does not take place. The resulting structure may be compared with ordinary glass which is an unstable structure able to form crystals under appropriate conditions. In addition, due to the rapid cooling of the material, the formation of the nucleation centers is avoided. From macroscopic point of view, the material is isotropic, which means that the material may be magnetized in any direction. Figure 5 and 6 depict the process of manufacturing of amorphous metals and the final product, respectively. Amorphous metals for applications in electrical machines are alloys composed mainly of Iron, with the addition of materials such as Silicon, Boron, Manganese and Carbon.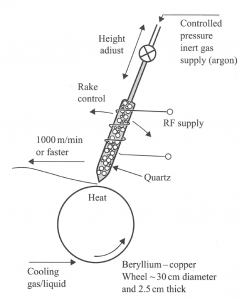
Figure 5. Melt-spinning diagram for the production of amorphous steel [4].
Figure 6. Finished amorphous ribbon [4].
The superior properties of amorphous metal arise from the thinness (e.g. 25 µm thick) and high electrical resistivity of the alloy (e.g. over 100 µΩ·cm), which restrains eddy currents [3]. Additionally, domain walls can move freely through the random atomic structure. The rapid cooling results in a strip which is highly stressed and requires a stress-relief anneal. A low temperature of approximately 250 degrees Celsius, must be used to avoid destructive crystallization of the metal. Core losses in amorphous steel are around 1/3 of those for grain-oriented SiFe. However, the cost of producing amorphous metal and the problems of handling it and avoiding compressive stress, which might increase the losses, causes its widespread use for large machines to be limited. Hence, the project: “Recyclable Electrical Machine Designs with 3D-Flux and Non-Traditional Materials” looks for an alternative use of amorphous steel. This project belongs to Work Package 3 of DEMETER project. Stay tuned for more information. Some interesting links about amorphous steel and its properties:
Cheers,
Adolfo.
Glossary [5]
Core losses: combined hysteresis and eddy current losses in a material.
Winding: a collection of connected coils.
Eddy currents: currents induced in electrically conducting material by a changing magnetic field, produces energy loss in the material.
Eddy current losses: energy losses due to eddy currents.
Hysteresis: a property of magnetic materials where the flux density in a material is a function of the history of the field intensity across the material, produces energy loss in a material.
Hysteresis losses energy losses due to hysteresis.
Permeability: a material property that describes how easily magnetic field flows through the material, analogous to how conductivity describes how easily current flows through a material.
Flux: magnetic field fluid, a scalar quantity describing the net fluid passing through an area.
Flux density: the density of the magnetic field fluid at a point in space, a spatial vector quantity.
Bibliography
[1] J. Soulard, “Design of Permanent Magnet Synchronous Machines- EJ2221.” Class Lectures. KTH- Royal Institute of Technology, September 2014. [2] P. Beckley. “History of the development of electrical steels” in Electrical Steels for Rotating Machines, IEE power and energy series; no 37. Ed. London: The institution of Electrical Engineers, 2002, pp. 197-202. [3] P. Beckley. “High-frequency applications” in Electrical Steels for Rotating Machines, IEE power and energy series; no 37. Ed. London: The Institution of Electrical Engineers, 2002, pp. 85-98. [4] P. Beckley. “Competing materials” in Electrical Steels for Rotating Machines, IEE power and energy series; no 37. Ed. London: The institution of Electrical Engineers, 2002, pp. 197-202. [5] D. Hanselman, “Appendix E,” in Brushless Permanent Magnet Motor Design, Magna Physics Publishing, second ed., 2006, pp. 373-379.
